PCA : Principal Component Analysis (PCA)¶
-
class
tesfdmtools.methods.PCA.PCA(n_components=10)[source]¶ Class for PCA analysis
-
fit_transform(data)[source]¶ Enter data into the PCA analysis.
- Args:
- data = matrix with data: data(jrow,iax)
jrow = data record number
iax = data record axis
- Returns:
data = transformed data in eigenvector space
- Properties:
components_ = eigenvectors
explained_variance_ratio_ = relative weights of eigenvectors
-
-
tesfdmtools.methods.PCA.cov(m, y=None, rowvar=1, bias=0, ddof=None)[source]¶ Estimate a covariance matrix, given data.
Covariance indicates the level to which two variables vary together. If we examine N-dimensional samples,
![X = [x_1, x_2, ... x_N]^T](../_images/math/07a703312fc8ba5a79fb6bd6dcea46ee788f996c.png) ,
then the covariance matrix element
,
then the covariance matrix element 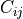 is the covariance of
is the covariance of
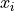 and
and 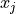 . The element
. The element 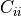 is the variance
of
is the variance
of 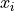 .
.- Args:
- m = array_like
A 1-D or 2-D array containing multiple variables and observations. Each row of m represents a variable, and each column a single observation of all those variables. Also see rowvar below.
- y = array_like, optional
An additional set of variables and observations. y has the same form as that of m.
- rowvar = int, optional
If rowvar is non-zero (default), then each row represents a variable, with observations in the columns. Otherwise, the relationship is transposed: each column represents a variable, while the rows contain observations.
- bias = int, optional
Default normalization is by
(N - 1), whereNis the number of observations given (unbiased estimate). If bias is 1, then normalization is byN. These values can be overridden by using the keywordddofin numpy versions >= 1.5.
- ddof = int, optional
New in version 1.5.
If not
Nonenormalization is by(N - ddof), whereNis the number of observations; this overrides the value implied bybias. The default value isNone.
- Returns:
- out = ndarray
The covariance matrix of the variables.
corrcoef : Normalized covariance matrix
Consider two variables,
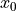 and
and 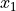 , which
correlate perfectly, but in opposite directions:
, which
correlate perfectly, but in opposite directions:>>> x = np.array([[0, 2], [1, 1], [2, 0]]).T >>> x array([[0, 1, 2], [2, 1, 0]])
Note how
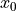 increases while
increases while 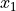 decreases. The covariance
matrix shows this clearly:
decreases. The covariance
matrix shows this clearly:>>> np.cov(x) array([[ 1., -1.], [-1., 1.]])
Note that element
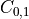 , which shows the correlation between
, which shows the correlation between
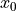 and
and 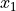 , is negative.
, is negative.Further, note how x and y are combined:
>>> x = [-2.1, -1, 4.3] >>> y = [3, 1.1, 0.12] >>> X = np.vstack((x,y)) >>> print np.cov(X) [[ 11.71 -4.286 ] [ -4.286 2.14413333]] >>> print np.cov(x, y) [[ 11.71 -4.286 ] [ -4.286 2.14413333]] >>> print np.cov(x) 11.71